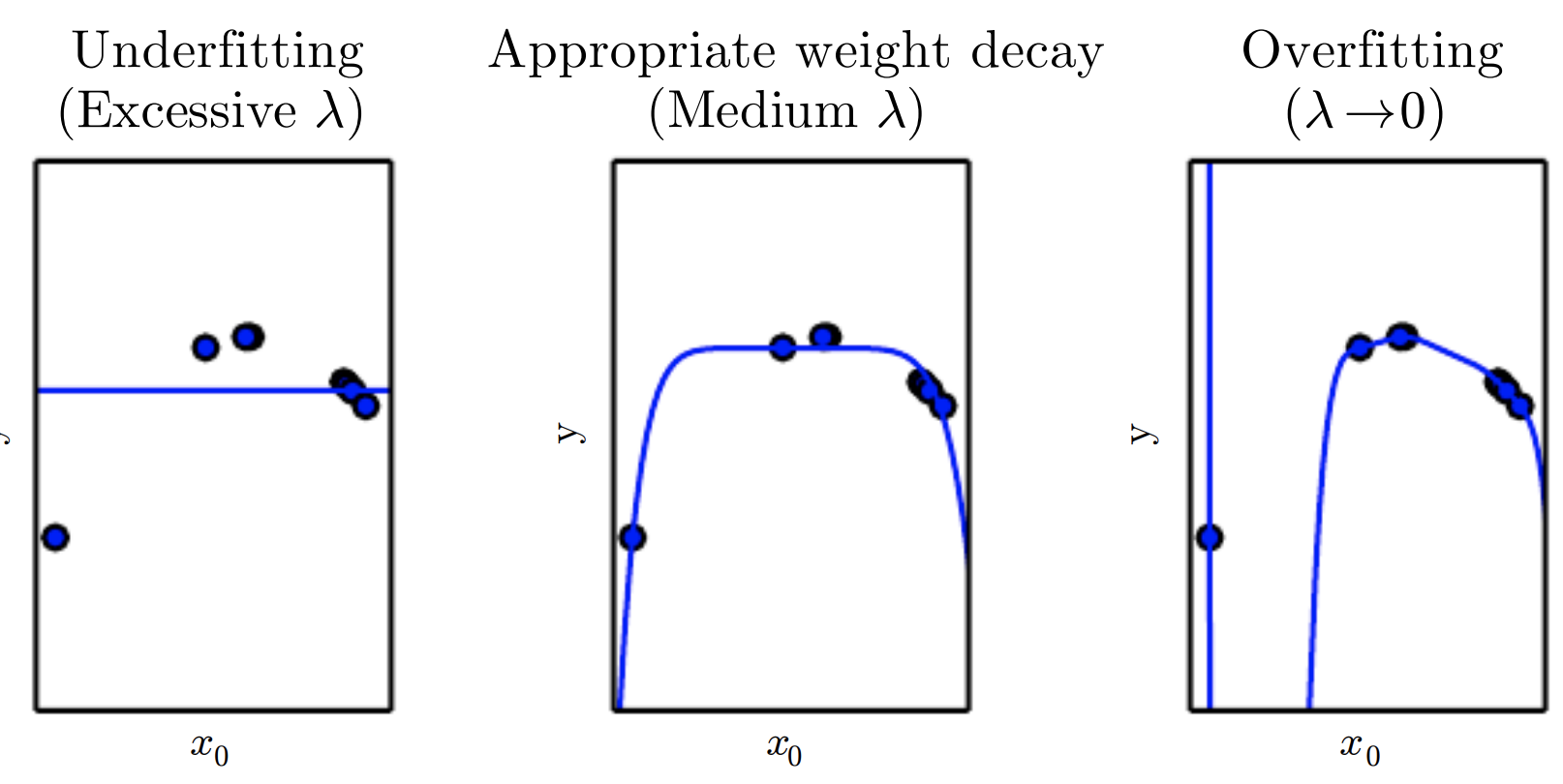
Weight Decay, or $L_{2}$ Regularization, is a regularization technique applied to the weights of a neural network. We minimize a loss function compromising both the primary loss function and a penalty on the $L_{2}$ Norm of the weights:
$$L_{new}\left(w\right) = L_{original}\left(w\right) + \lambda{w^{T}w}$$
where $\lambda$ is a value determining the strength of the penalty (encouraging smaller weights).
Weight decay can be incorporated directly into the weight update rule, rather than just implicitly by defining it through to objective function. Often weight decay refers to the implementation where we specify it directly in the weight update rule (whereas L2 regularization is usually the implementation which is specified in the objective function).